感谢 Felix Cai 对 MACI 和隐私投票中多个问题的讨论。
这篇文章将展示基于 2-of-2 MPC 技术的 MACI 匿名化方案的具体实现。本文核心内容主要分为三个部分:从任意算法到逻辑电路的实现;从逻辑电路到混淆电路的实现;利用不经意传输实现多方安全计算。最后,我们总结基于多方安全计算的匿名化方案。
算法
在 MACI 系统中,操作员 Operator(记为 deactivate[],其元素个数与 registry 数组中的元素个数相同。数组中每个位置的编号代表了 key 值(用户的编号),而每个位置存储着对应的公钥。为了更好地理解 deactivate[] 数组,可参考如下例子:在 deactivate[] 数组中,假设 registry 中的用户 deactivate[] 数组中的第一个元素)发起了 deactivate key 操作,操作员 deactivate[] 数组中的第一个位置填入 registry 数组中第一个位置所包含的 value 值(用户 deactivate[] 数组中的第二个元素的值为 0。这样一来, deactivate[] 数组的元素个数和 registry 数组中的元素个数相同就可以理解了。
现在,为了实现 MACI 系统对管理员的匿名性,需要设计一个 2-of-2 的 MPC 方案来实现以下两个性质:
- 假设拥有
的用户 想将 更改为 ,他需要实现让操作员(记为 )不知道更新的 是替换的 。 - 拥有
的用户(称为 )不能知道 deactivate[]数组中的除了外的其他任何元素。
先暂且不考虑这两个要实现的目标。先考虑更换密钥的操作: deactivate[] 数组中属于
因此,deactivate[] 数组中,是否有元素
根据上述逻辑,我们先设计一份伪代码来实现这个操作,如下:
用户 deactivate[] 数组中的值进行比较,得出输出(deactivate[] 数组中,则执行公钥更换操作;否则就不执行。
现在,假设 deactivate[]:
function findElement(array, PK_1, PK_1′) {
for (let i = 1; i < array.length; i++) {
if (array[i] === PK_1) {
return PK_1′;
}
}
return false;
}fn find_element(array: &[i32], a: i32, b: i32) -> bool {
let mut result = false;
for i in 1..array.len() {
result = result || (array[i] == a && b == a);
}
result
}至此,我们已经实现了简单的在明文下的公钥更换操作。下面,我们将介绍逻辑电路的生成原理,混淆电路的生成原理,以及混淆电路输入的加密。这些步骤是实现上述 MACI 匿名性质 1 的关键,也就是让 deactivate[] 数组中的哪一个元素。
逻辑电路的生成原理
现在需要将上述算法转换成逻辑电路,转换的逻辑就是用逻辑运算符构造逻辑电路。一个逻辑运算符(如 0 和 1 两种可能。一个
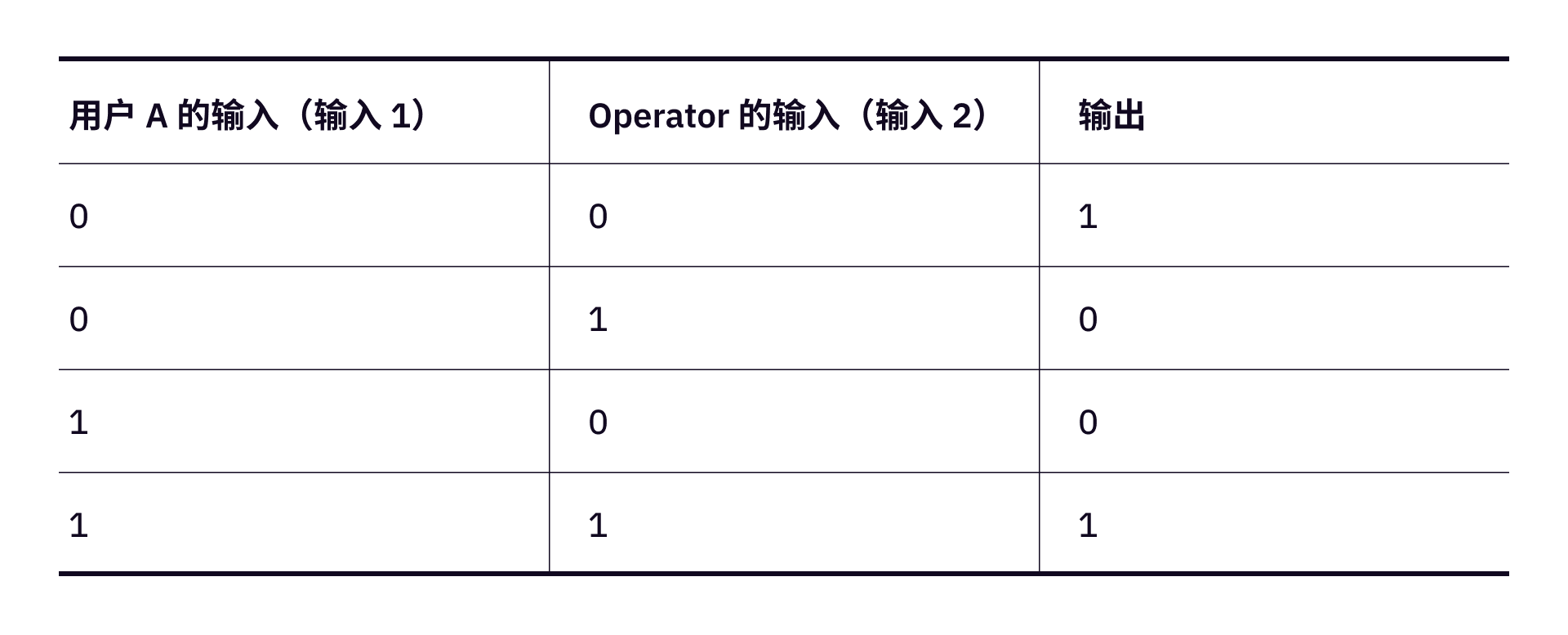
打个比方,在上面的例子中,假设 deactivate[] 中的元素个数是二,由 deactivate[] 数组中的所有元素。
为了简单起见,暂且假设一个公钥由二位二进制数来表示(实际的公钥是 256 位二进制数)。那么,现在就需要用用户 deactivate[] 数组中的二把公钥。因此,需要对比二次。
对于一把公钥的对比,由于假设一把公钥有二位,那么就需要两个
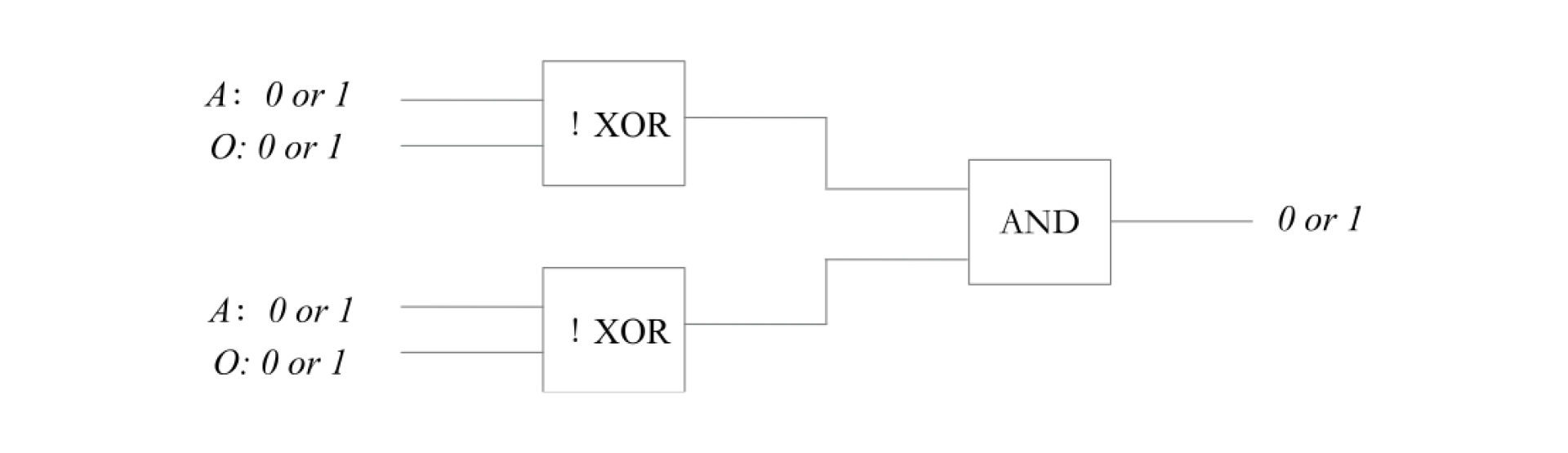
逻辑电路由逻辑门组成,逻辑电路中的逻辑门被分为
因此,两个这样的子逻辑电路再配上一个
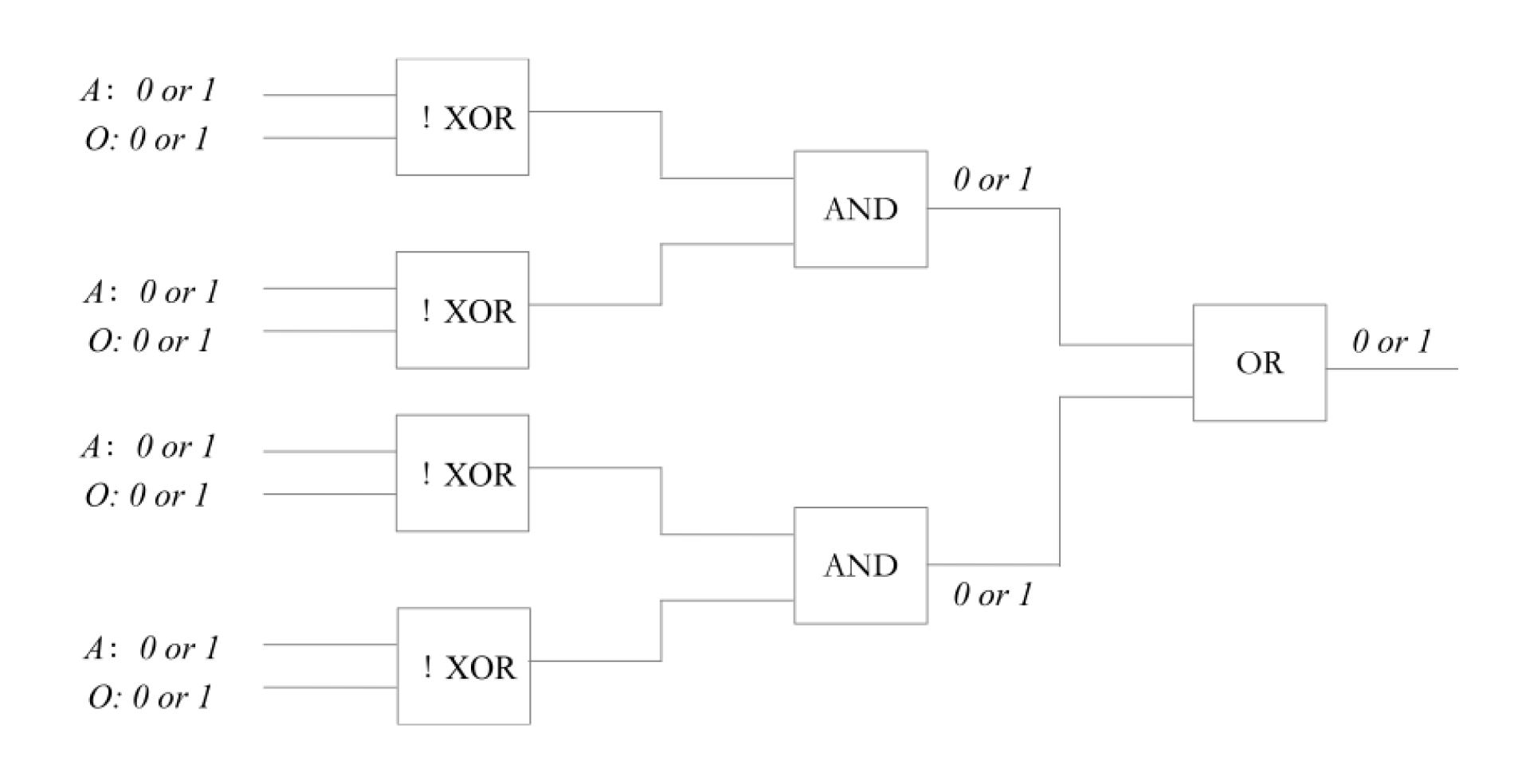
为了便于理解,根据上述的假设,我们可以设计这样一个例子,假设用户 10,那么用户 1,在上图中下方的 0。同时,用户 1,在上图中下方的 0(用户
假设 deactivate[] 数组中的第一个和第二个元素分别是 10、11。那么,1,在第一个逻辑子电路中下方的 0。同时,1,在第二个逻辑子电路中下方的 1(
这样一来,第一个 1,输出自然也是 1。同理,第二个 0,输出自然也是 1(根据表一的计算规则可知)。这样一来,1,输出也是 1。因此,通过执行第一个逻辑子电路的对比(即对比用户 deactivate[] 数组中第一个元素对第一个逻辑子电路的输入),得到的输出结果是 1,从而可以证明,用户 A 的输入和 deactivate[] 数组中的第一个元素是完全一致的(都是 10),因此可以证明用户 deactivate[] 数组中。
逻辑电路的生成工具
在现实中,为了让一个固定的算法转换成逻辑电路,需要用到一些工具,如
- Verilog HDL 和 VHDL:这两种硬件描述语言被广泛用于数字电路的设计和仿真,可以使用它们来描述算法的行为,并将其转换为逻辑电路的形式。这些语言都支持从高级语言(如C、C++ 和 Java)转换为硬件描述语言的形式。使用 Verilog 或 VHDL 需要一定的硬件设计和编程经验。
- Xilinx Vivado Design Suite:这是一款商业软件,用于 FPGA(现场可编程门阵列)的设计和开发。它提供了一个综合工具,可以将高级语言或 RTL(寄存器传输级)代码转换为逻辑电路的形式。它支持多种编程语言,包括 C、C++、SystemC、Verilog 和 VHDL 等。
- Yosys:这是一款开源的 EDA(电子设计自动化)工具,用于数字电路的设计和仿真。它支持从 Verilog 和 VHDL 等硬件描述语言转换为逻辑电路的形式。它也支持从高级语言(如 C、C++ 和 Python)转换为 RTL 代码,然后转换为逻辑电路的形式。
混淆电路(Garbled Circuit)
逻辑门的加密(混淆)
回到现在的例子中,因为我们的公钥在 deactivate[] 数组中都是有序号的(序号等价于用户的编号),且数组 deactivate[] 中的最大元素个数是有上限的(用户的个数)。因此,假设最大元素个数是
由于逻辑电路在每一个 epoch 中(一个 epoch 是区块链更新 registry 中元素的一个周期)是固定的,那么,所有用户都可以使用这个早已经生成好的,并存储在区块链中的逻辑电路。在本文例子中,由于 deactivate[] 数组中只有两个元素,因此子电路只有两个(每个子电路对应于一次公钥的对比)。
注:在一个 epoch 中,registry 数组中元素个数是固定的,因此用户的输入和数组中的元素的对比次数是固定的,因此逻辑子电路的个数是确定的,且逻辑子电路是事先可以确定好的,因此整个逻辑电路是唯一确定的。
接下来,就是将逻辑电路的每一个输入进行加密,然后将每一个逻辑门进行混淆。
先考虑加密。加密这个动作是由用户 0 和 1 用加密值表示。注意,最终的根逻辑门的输出不需要进行加密,在本案例中,就是 0(对比失败),和 1(更换新的公钥)。如图所示:
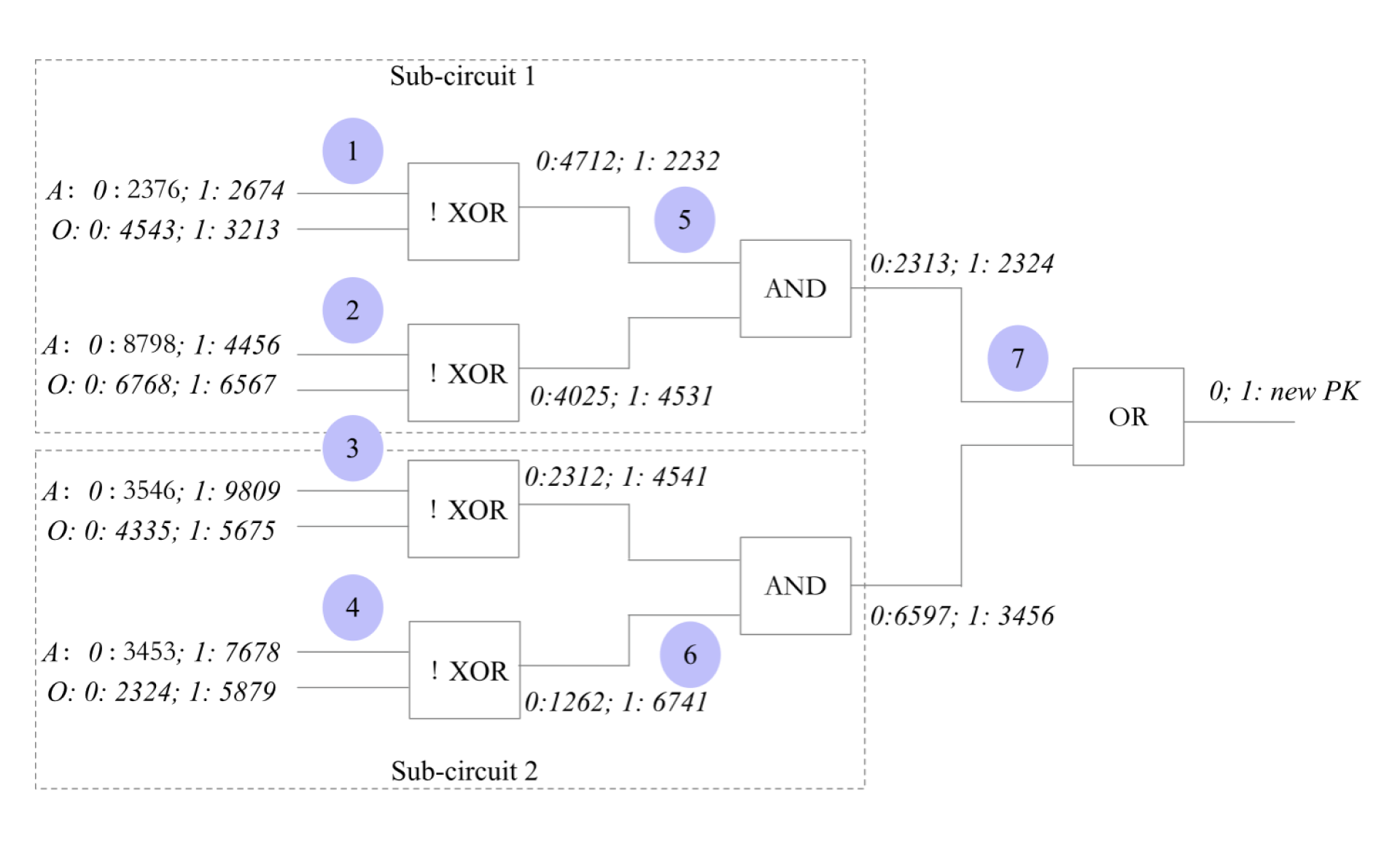
逻辑电路中的每一条引线的 0 和 1 都用加密值代替。同时,每一个逻辑电路都有一个固定的编号(这个是所有人都已知的)。例如,编号 1、2、5 就构成了一个子电路 1(比较用户的公钥和数组中的第一把公钥)。
基于此,将逻辑电路的每一个逻辑门的输入和输出(除了根逻辑门)进行加密后,在 Operator 的视角里,对于加密后的逻辑电路,他就不知道每个逻辑门的输入数字(加密值)对应的明文(是 0 还是 1)。
输入加密的方法
在混淆电路中,为每个输入值生成两个随机 key 的过程通常是使用伪随机数生成器(PRNG)来实现的。常用的生成随机 key 的实现和库有很多,例如 OpenSSL、Crypto++、libsodium 等。
输出加密的方法
基于伪随机函数 PRF 的方法是 Yao 的混淆电路中实现对输出二进制数 0 和 1 的加密的主要方法之一。具体来说,这种方法可以实现对每个逻辑门的输出进行加密,保证了数据的机密性和可靠性。
在基于 PRF 的方法中,每个逻辑门的输出都被混淆成为一组包含多个 label 的二元组,其中每个 label 都是一个随机的 01 字符串。在生成每个 label 时,可以使用伪随机函数(PRF)来实现。具体来说,可以使用一个密钥和输入值(如 0 或 1)作为 PRF 的输入,然后得到一个随机的 01 字符串作为 label。由于 PRF 是一种可以模拟真正随机数的算法,因此生成的 label 具有高度的随机性和不可预测性,保证了数据的机密性和安全性。
在混淆输出时,可以将每个逻辑门的输出表示为一个包含两个 label 的二元组(如 {label0, label1})。其中,当输入为 0 时,使用 label0 作为输出;当输入为 1 时,使用 label1 作为输出。在将逻辑门的输出发送给下一个参与方时,只发送一个包含正确 label 的二元组,保证了数据的机密性和保密性。常见的 PRF 包括 HMAC、SHA、AES 等。
需要注意的是,对逻辑门的输出采用上述方法的目的是为了便于不经意传输(oblivious transfer)的实现。
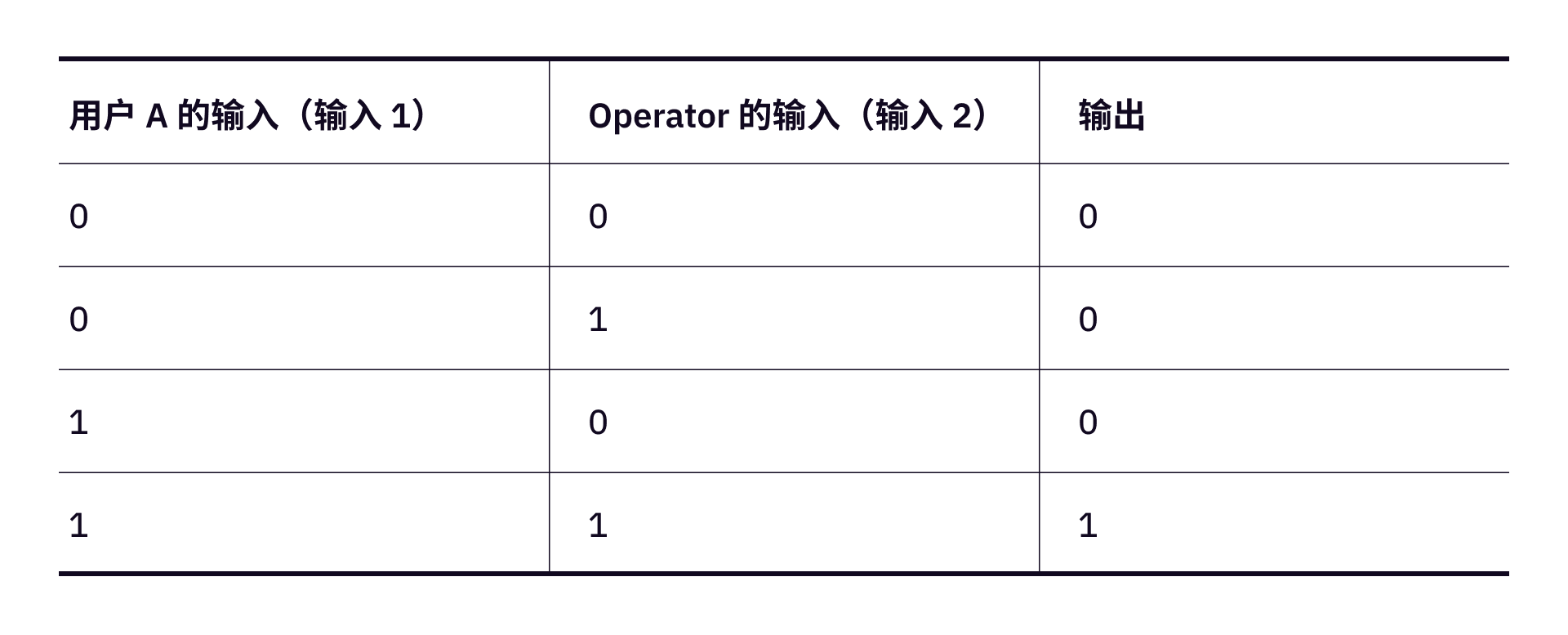
现在,我们来举个例子:下面的图是对
- 第一行的输出
0加密成, - 第二行的输出
0加密成, - 第三行的输出
0加密成, - 第四行的输出
1加密成。
其中
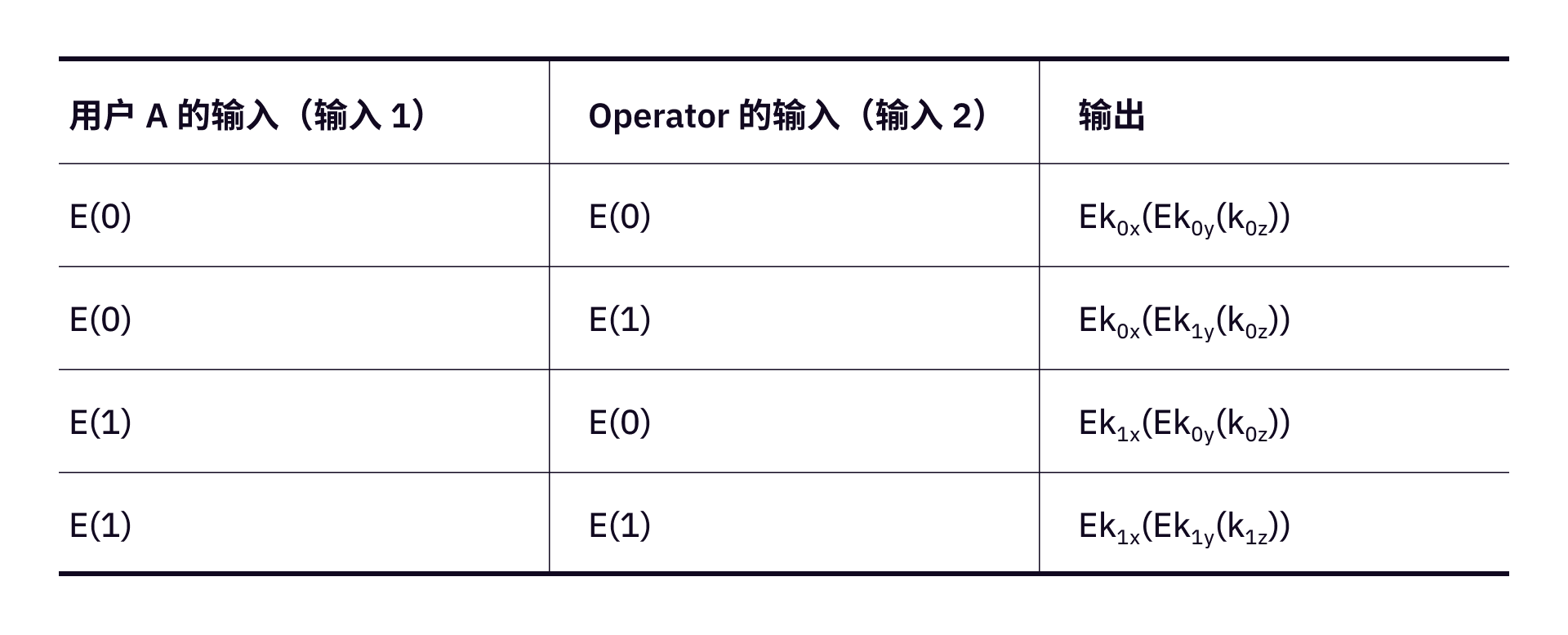
这里其实就可以推导不经意传输过程了。比如,用户 A 将这四个输出——
——分别发送给
此时对于
用户 A 输入的生成
现在,我们继续假设,用户 10,而数组中的二把公钥(编号分别为 0、1)的数值分别是 11, 10。也就是说用户
接着,用户将自己的输入,分别输入到两个子电路中(sub-circuit 1 和 2)。用户在第一个逻辑子电路(1、2、5)中进行输入。他的输入是:在编号为 1 的逻辑门输入 2674(代表二进制数 1);在编号为 2 的逻辑门输入 8798(代表二进制数 0)。用户在第二个逻辑子电路(3、4、6)中进行输入。那么,他的输入是:在编号为 3 的逻辑门中输入 9809(代表二进制数 1);在编号为 4 的逻辑门中输入 3453(代表二进制数 0)。
那么,用户 2674, 8798 和 9809, 3453 对应的明文均是二进制数 1, 0。而对于 2674, 8798 和 9809, 3453 对应的明文均有四种可能 0, 0、0, 1、1, 0、1, 1。如果密文的长度从二位变成 256 位,那么明文的可能性就有
电路混淆
接下来的步骤就是将逻辑电路进行混淆。

对于一个
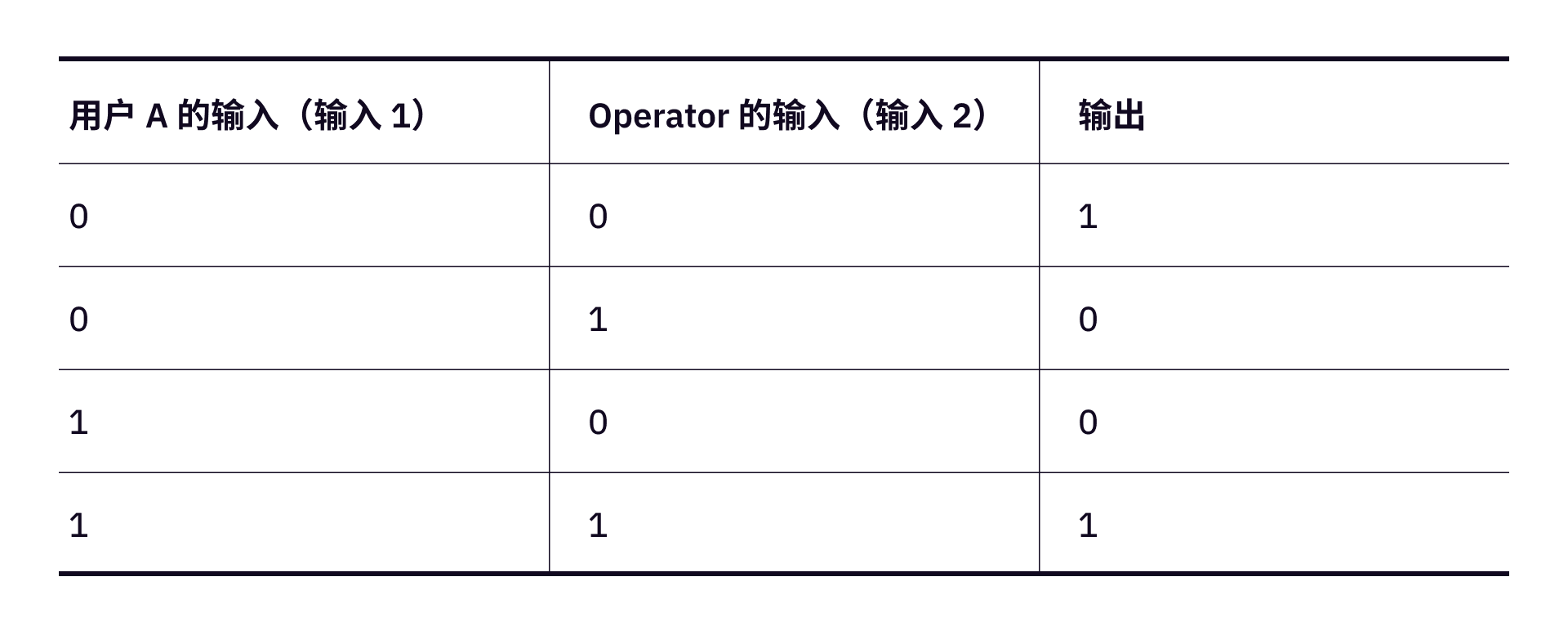
现在,这个加密版本的
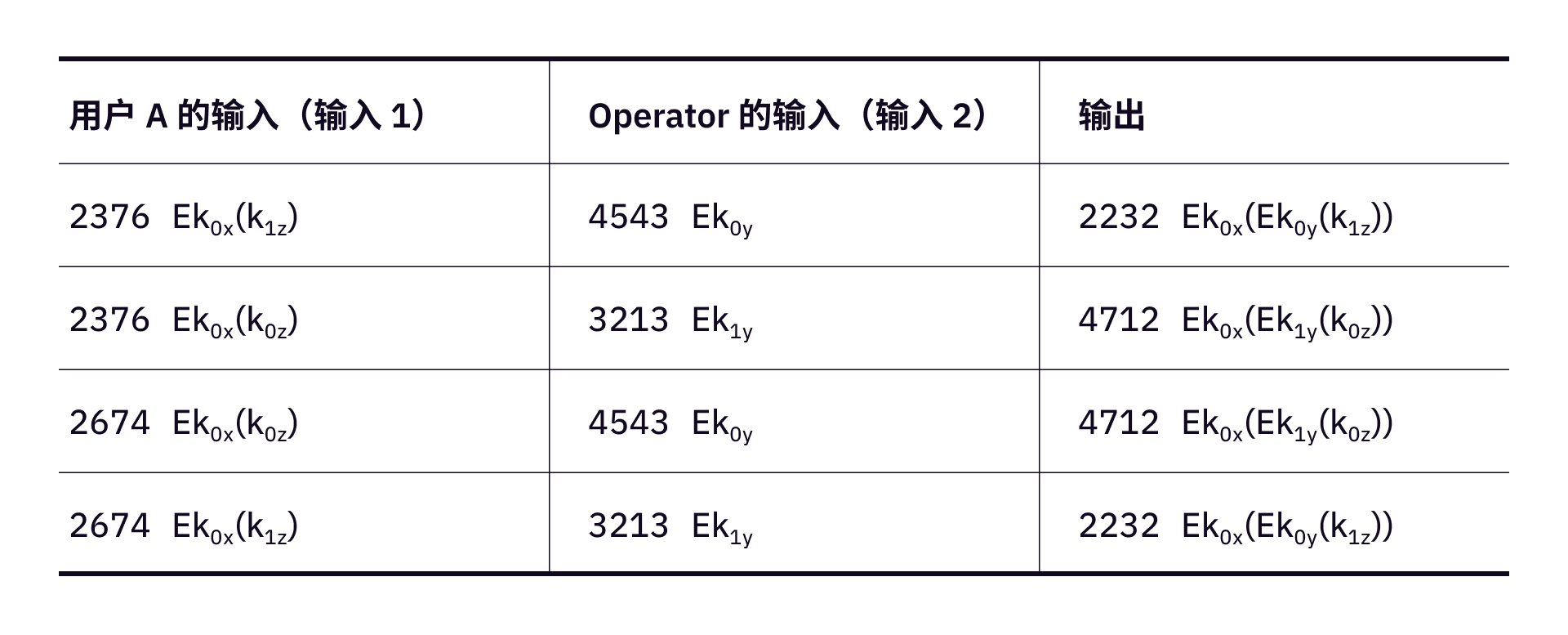
由于上面的没有打乱顺序,2376 对应于用户的输入 0,2674 对应于用户的输入 1。
现在来打乱表二的顺序,变成表三(混淆版本的逻辑门)。
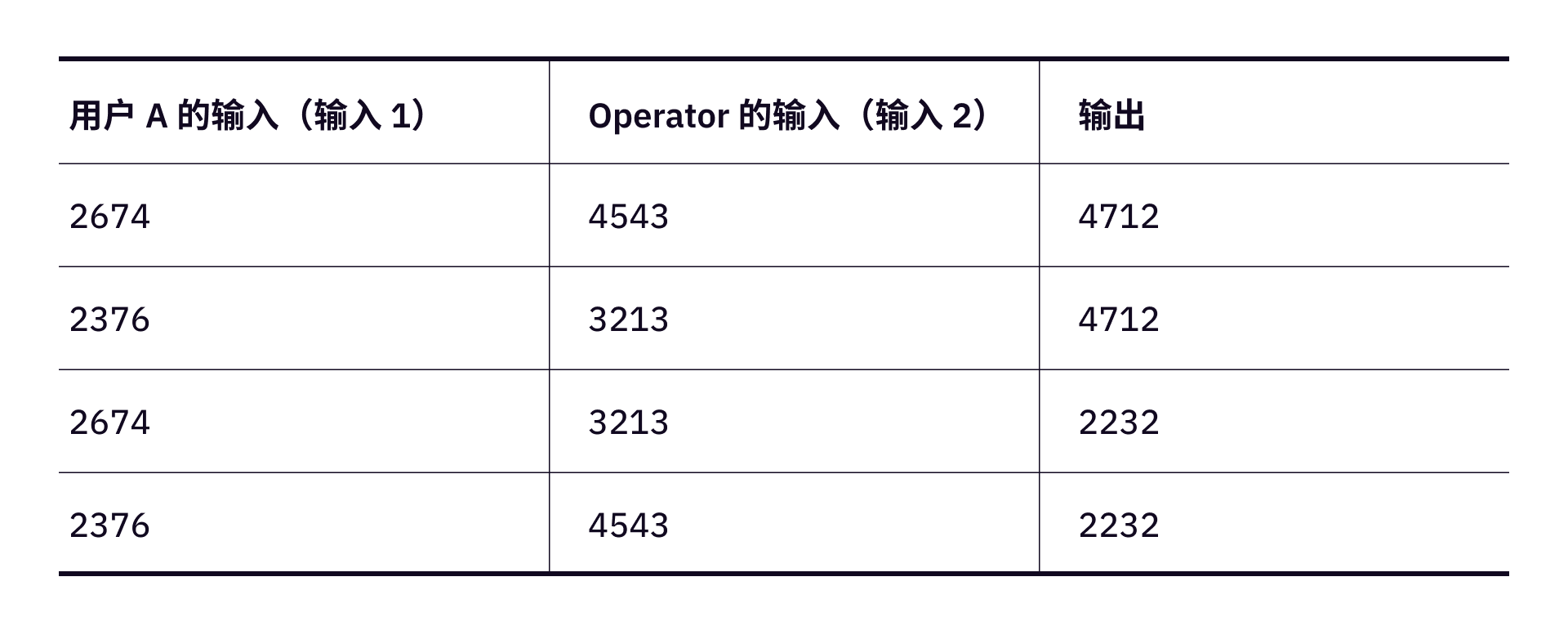
这样一来,根据这个表格的排序可能性,0 还是 1。
第一次通信
用户将这七个逻辑门所对应的混淆之后的逻辑门表发送给 2674, 8798)和 9809, 3453)还将自己的新公钥
此刻,我们做一个总结,
到这里为止,我们已经实现了第一个目的,通过设计混淆电路和对混淆电路输入的加密,deactivate[] 数组中除了
不经意传输(Oblivious Transfer)
由于对于每个子电路,11(也就是说对于逻辑门 1 和逻辑门 2,1);第二个子电路,10(也就是说对于逻辑门 3 和逻辑门 4,1 和 0)。但是,由于 0 哪个代表 1(如对于逻辑门 1 的 4543 和 3213 这两个加密值,4543 代表 0,3213 代表 1),因此,
此时,我们需要回顾两个一定要保证的性质:
- 假设拥有
的用户 1 想将 更改为 ,他需要实现让操作员(记为 )不知道更新的 是替换的 。 - 拥有
的用户(称为 )不能知道 deactivate[]数组中的除了外的其他任何元素。
因此,在
下面详述 OT 的全过程。以编号为 1 的逻辑门也就是 1。
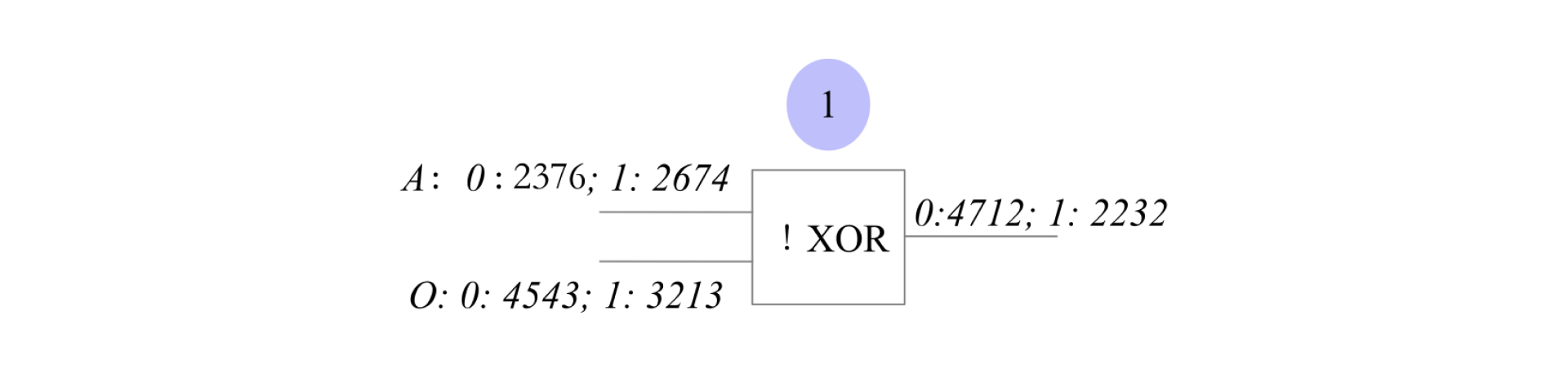
这个时候,2674(2674 是啥意思),1 的加密值到底是 4543,还是 3213。但是,为了保证第二条性质,1 的加密值。同理,0 等于 4543 以及 1 等于 3213 告诉
生成一个哈希值 。 这个哈希值已经于之前传输给了 。 将 和 发送给 。 验证 是否成立。如果成立,则进行下一步,否则则不需要回复 。
对这一步进行说明,只要这个
值没有后门,那么,对于 来说,他想要满足公式 ,他就需要先生成一把私钥 ,然后生成公钥 ,然后再通过 得到 。也就是说, 只能拥有 和 这两把公钥中的一把私钥。否则,就意味着 能破解 DH 离散困难。即 能从公式 中求解出 。
利用密码学协议(例如 ElGamal 协议)传输消息。 选择一个随机数 。将 和 发送给 。 - 由于
只有 和 这两把公钥中的一把私钥,因此 可以求解出其中一个秘密。但是 并不知道 求解出了哪个秘密。这保证了特性 2。
上述三个步骤,满足了第二个性质,但是没有满足第一个性质,也就是说,1,但是,也暴露了另一个明文 0。这样一来,混淆逻辑门表就暴露了很多信息给
对于此的解决方案是,1 的加密值是 4543 还是 3213。他只知道,对于编号为 1 的逻辑门,他得到的输出是 2232。但是他又不知道,2232 代表 0 还是代表 1。
从对一个逻辑门的 OT 通信可以看出整个 OT 通信的全貌,即每个逻辑门的 OT 通信都是如此,且在一次 OT 通信过程中全部完成。这样,
方案改进
上述方案中,需要且可以改进的地方有很多。例如,改进算法设计,降低算法的复杂度;改进逻辑电路的设计,让逻辑电路变得更加简单(减少门的个数,减少通信是需要传递的信息);增加方案的安全性,加大破解方案的计算复杂度;让交互变成非交互。
算法和逻辑电路的改进
当前逻辑电路实现的比较算法的复杂度是
但是,如果采用 Merkle Patricia Tree 的数据结构的话,对比的次数要少很多(这是因为对于 256 位的公钥来说,形成的 MPT 一定是稀疏的,因此,可能筛选二到三轮就可以筛选出想要的值)。那么,一旦算法计算复杂度下降了,逻辑电路的设计也就要简单很多。
逻辑电路的设计也有化简的可能性。

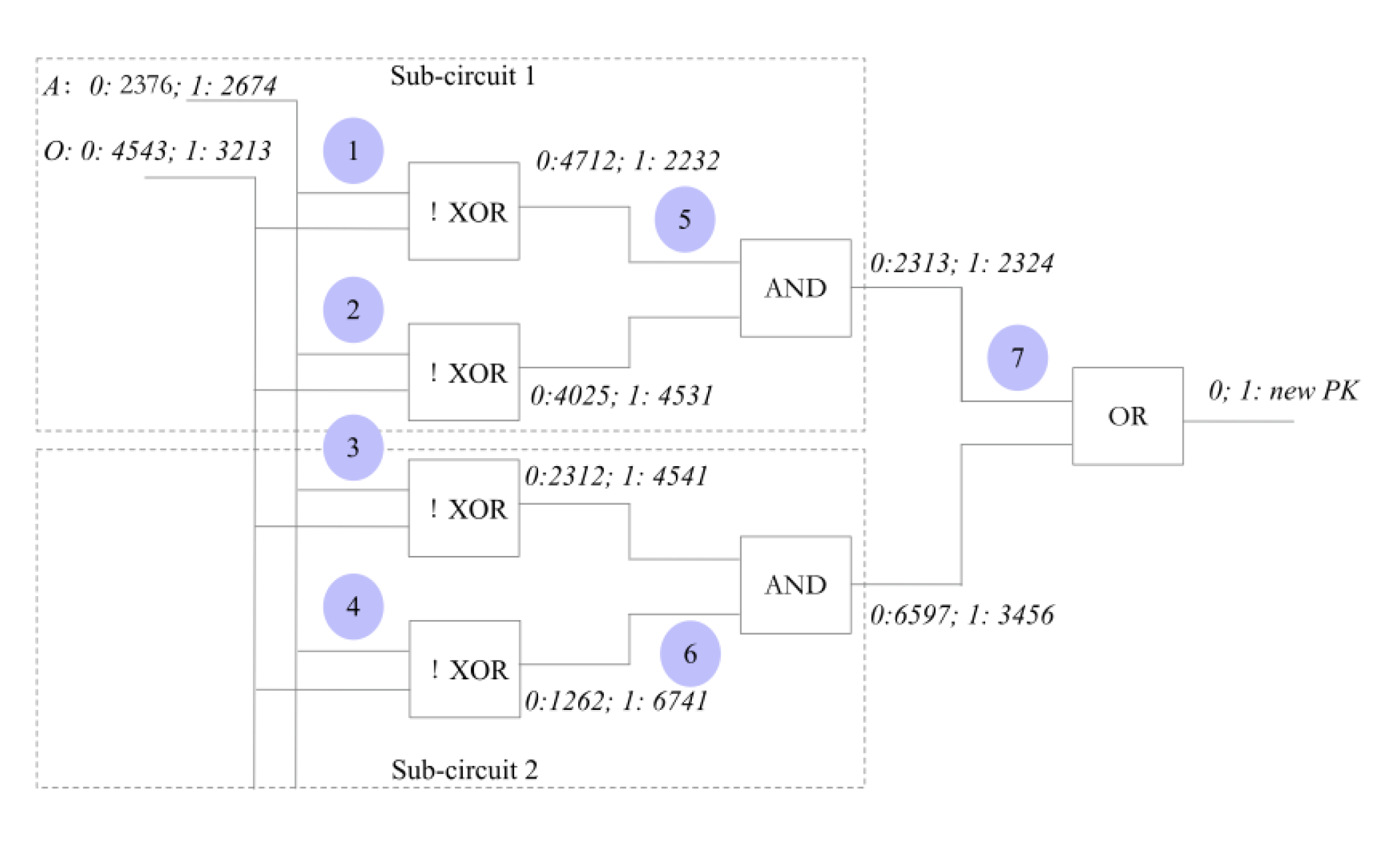
这样的化简可以让输入变少。
增加安全性
对于安全性,就是需要让
如果 0,那么他得到的结果必然是 0,也就是说,他天然知道输出 0 的加密值,那么他就天然知道了 1 的加密值。同时,由于 1 的输出的加密值所在的行,不包含 0,否则就是 1。
为了解决这类问题,我们需要对输出全部进行加密。比如使用该种方法:上表中的四个输出值 0、0、0、1 分别加密为——
——这样一来,输出的四个值分别对应为四个不同的密文。因此,在此环境下,0 还是 1。但是,这种方法使得输出加密值的个数从二变成了四。通信复杂度会增大。
此外,非交互式的不经意传输协议也值得研究。
总结
上述方法首先不考虑需要实现 MACI 匿名化的两个目标,即在明文下设计一个算法,让
进而,使用不经意传输是实现第二个目的的方法。通过不经意传输,用户 deactivate[] 数组中的其他元素信息。同时,由于
最终,deactivate[] 数组中的元素和 registry 数组中的元素来更新 registry 数组并结束 epoch 和开启下一个 epoch。